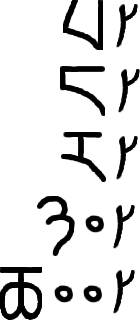Numbers in Seuna

In Seuna the number system uses base 8. Remember that all the numbers in this section are in octal.

Zero

Seuna has a symbol for zero (actually similar to our "o" but a bit smaller). It is called nyegatuna (gap symbol).

From 1 to 7

@aba	@iga	@oda	@ela	@uca	@aisa	@auka
one	two	three	four	five	six	seven

Seuna doesn't have separate symbols for the numbers 0 to 7, but instead uses letter symbols. Also a vertical slash is included. Every Seuna number must have a vertical slash. Unlike words which are written next to other words with no spaces in between, a number must be separated by spaces on either side.

From 10 to 77

108	@abau
208	@igau
308	@odau
408	@elau
508	@ucau
608	@aisau
708	@aukau

As with the basic numbers, the above numbers can be combined. @igaudau = "twenty or thirty". There is another form for the above numbers that specifies a range. For example @odaua specifies the range 30₈ to 37₈

Every number from 1 to 63 has its own unique word which can be worked out from the above tables. For example "twenty three" is pronounced as @igauda and written ;-

From 100 to 777

1008	@abai
2008	@igai
3008	@odai
4008	@elai
5008	@ucai
6008	@aisai
7008	@aukai

As with the other numbers, the above numbers can be combined. For example @elaicai = "four or five hundred".

The above set of numbers can also be modified to specify a range. For example @elaia specifies the range 400₈ to 477₈

As with the two digit numbers, every three digit number(i.e. 1 to 777) has its own unique word which can be worked out from the above tables. For example ;-

@ucaiba = 501₈

The 18 words denoting uncertainty

The first 6 are

1 or 2	@abiga
2 or 3	@igoda
3 or 4	@odela
4 or 5	@eluca
5 or 6	@ucaisa
6 or 7	@aisauka

Please note that, for example, @odela does not totally rule out the numbers 5 or 2.

These above words are often translated as "a few" or "several".

And we have 6 special words for the next rank of numbers i.e. "50 or 60" = @ucaisau

And another 6 for the next rank i.e. "300 or 400" = @igodai

These 18 words have a special notation or shorthand way of writing them. There are five examples below ;-

The top one is @abiga or "1 or 2"

The next one is @igoda or "2 or 3"

The next @odela or "3 or 4"

The next @elucau or "40 or 50"

And the last one is @ucaisai or "500 or 600".

feti or the vertical slash

The vertical slash that must come with all numbers, when unadorned with a superscript or a subscript, can function as a decimal point. Also when occurring at the left hand side of a number or in the middle of a number it is pronounced when speaking out the number. For example ;-

pronounced @iga feti @odai

pronounced feti @igaidau

Note that the above to examples are not pronounced @iga feti @oda or feti @iga @oda or feti @igauda. This is explained in the next section.

From 1000 to 10³⁶-1

10³⁶-1 = 777,777,777,777,777,777,777,777,777,777 .... remember the "10" and "30" are octal, not decimal.

We have already seen one way to write 501. There is also another equally valid (but rarely encountered) way to write 501. It is shown below.

To express numbers greater than 777, Seuna has a number of exponention terms. These never occur by themselves but must be proceded by one of the numbers 1 to 777. These exponential terms are each written using a small superscript letter placed over the vertical slash. They are in some ways equivalent to the S.I. prefixes kilo, Mega, giga etc..

83	m	mu
86	y	yu
89	j	ju
812	f	fu
815	p	pu
818	t	tu
821	w	wu
824	n	nu
827	h	hu

So for example;-

34y4 ce (pronounced : @odaula yu @elace) is about^* the population of the UK in 2008. Seuna has a special symbol (pronounced as "ce") which tells us the number is not exact, it is only accurate to three significant figures.

Usually we only deal with approximate numbers. However in some scientific situation you have long and accurately known numbers. For example 34y472m531 (pronounced : @odaula yu @elaikauga mu @ucaidauba). In these situations the letters divide the numbers up into sets of three ... a bit similar to how we use comma's to make long numbers easier to read.

^* If by some chance, the population of the UK was known to be exactly this number, then it would be represented by 34y4̴- (pronounced : @odaula yu @elatiki)

To show the exactness of a number

Three symbols that when placed over "letters", represent vowels, are used to give some idea of the exactness of a number.

The basic number above @oda mu @elai which we can say is "three thousand four hundred"(roughly).

The first word has the "i" vowel symbol after it. It would be pronounced @oda mu @elai tiki ... tiki simple means "exactly"

The second word has the "u" vowel symbol after it. It would be pronounced @oda mu @elai jubu ... jubu simple means "approximately". Note that this symbol is very similar to the symbol for zero. However as zero will never occur on the trailing edge of a number, there is no chance of misidentification.

The third word has the "a" vowel symbol after it. It would be pronounced @oda mu @elaia . This expression denote the range of numbers from 3,400 => 3,477.77777 ...

The fourth word would be pronounced @oda mu @elaicaua . This expression denote the range of numbers from 3,450 => 3,457.7777 ...

When @oda mu @elaicaua is followed by the locative case clitic, it mean one number in the range 3,450 => 3,457.7777 ...

From 1 to 10^-36-1

Of course there is also a way of representing numbers smaller than one, as well. The table below shows the symbols used for this.

8-3	m	mi
8-6	y	yi
8-9	j	ji
8-12	f	fi
8-15	p	pi
8-18	t	ti
8-21	w	wi
8-24	n	ni
8-27	h	hi

Now you can see the same letter is being used to write exponent values greater than one and also less than one. What is to stop confusion between the two sets ? Well for longish numbers with two or more exponent values, the relative order of the exponents should tell you if we are dealing with a greater than one situation, or a less than one situation. For example 34y4̴72m531 must be greater than one, and 34m4̴72y531 must be less than one. However how do we distinguish between numbers that have only one exponent ? Well in these cases we would put a decimal point to the left of the numbers that are smaller than one. The decimal point symbol is a near-vertical dash(represented here by "/"). For example /34y4̴⁓ is a number smaller than one.

Note;- The numbers get there magnitude value from the letter and not the decimal point. Only if there is no letter, do they take there magnitude value from the decimal point. For example /34 would equal (3*8^-1)+(4*8^-2). Whereas /34y would equal (3*8^-5)+(4*8^-6).

And even bigger numbers

The two sets of exponent terms given above can be expanded somewhat to specify a bigger range of numbers. A symbol pronounced mua (written as the Seuna symbol for "m" with a small slash under it) representing 8³⁰ comes after the symbol pronounced hu. Other large exponents are generated in a similar manner up to a symbol pronounced hua representing 8⁵⁴.

And we can expand these terms even more. A symbol pronounced muan (written as the Seuna symbol for "m" with two small slashes under it) representing 8⁵⁷ comes after the symbol pronounced hua. Other large exponents are generated in a similar manner up to a symbol pronounced huan representing 8⁸¹.

In a similar manner the small exponents can be expanded to 8^-81. This is pronounced hian and written the same as huan.

Numbers outside the above ranges are not specified.

Fractions

a unit	haban
a half	higan
a third	hodan
a fourth	helan
a fifth	hucan
a sixth	haisan
a seventh	haukan

Ordinal numbers

Ordinal numbers are adjectives so come after the word that they qualify.

@oda dwolo = three houses

dwolo @odas = the third house

Nouns from numbers

klolo = wheel, klolaga = bicycle ?? kloli = vehicle ??

Negatives numbers

A negative is represented by putting "back/backwards" after the number.

Imaginary numbers

An imaginary number is represented by putting "side/sideways" or "rightside" or "leftside" after the number.

Mathematical operations

Addition

Western mathematical notation	Which is pronounced
2 + 3 = 5	two and three is five
Seuna mathematical notation	Which is pronounced
2,3>5	aga ada ro aca

Subtraction

For subtraction, or addition which inviolves negative numbers, each number must be followed by either "forward" or "backward" depending upon whether the number is possitive or negative.

Multiplication

There is a particle je which is placed between words to be multiplied.

Western mathematical notation	Which is pronounced
2 x 3 = 5	two times three is five
Seuna mathematical notation	Which is pronounced
2+3>5	aga je ada ro aca

Division

15 divided by 5 is 3 ............. 15 shared 3ji is 5

tonda means "to add" or "addition", and jemba means "to multiply" or "multiplication". ??? tondua = subtraction, jembua = division ???

Index

1. Introduction to Seuna
2. Seuna : Chapter 1
3. Seuna word shape
4. The script of Seuna
5. Seuna sentence structure
6. Seuna pronouns
7. Seuna nouns
8. Seuna verbs (1)
9. Seuna adjectives
10. Seuna demonstratives
11. Seuna verbs (2)
12. Asking a question in Seuna
13. Seuna relative clauses
14. Seuna verbs (3)
15. Methods for deriving words in Seuna
16. List of all Seuna derivational affixes
17. Numbers in Seuna
18. Naming people in Seuna
19. The Seuna calendar
20. Seuna units